Privacy Enhancing Technologies (PETs) enable data scientists to perform computations on encrypted data sets in a privacy-preserving manner. There are several PETs, each of which has a different role in data protection and analysis. In this blog, I will provide a brief explanation of one of them, homomorphic encryption (HE), from the cryptographerβs perspective β including a basic explanation of how it works and the difference between partially, leveled and fully homomorphic encryption (FHE).
Homomorphic encryption is a way to perform computations on encrypted data without ever decrypting it first.
An example of a partially homomorphic encryption scheme is the well-known RSA encryption scheme. RSA has the property where if you multiply the encryption of π and the encryption of π, you obtain the encryption of π β π. To see why, we describe the scheme below:
RSA consists of public key (π, π) and private key π. Encryptions of messages π and π are defined below:
ππ = ππ (πππ π)
ππ = ππ (πππ π).
Multiplying the two ciphertexts gives
πππ = ππ β ππ = (π β π)π (πππ π).
In practice, RSA is often used with a padding scheme, so the ciphertext ππ will consist of ππ with zeros padded at the end. This destroys the homomorphic properties of the scheme. However, if a user wished, they could use RSA without the padding as a partially homomorphic encryption scheme.
For many applications, being able to simply multiply two ciphertexts is not enough. A leveled fully homomorphic encryption scheme is an encryption scheme that satisfies three properties:
We give an example of a leveled fully homomorphic encryption scheme below. You can find an implementation of the BFV (Brakerski-Fan-Vercauteren) scheme, invented in 2012 and described below, in our open-source library PALISADE.
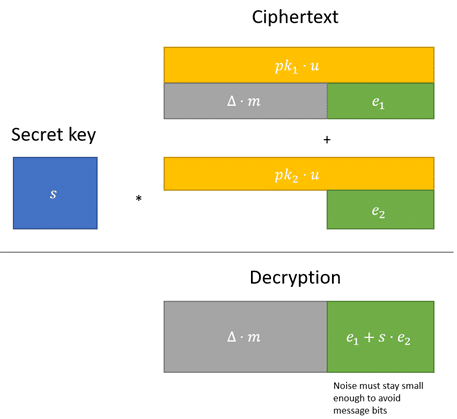
In order to satisfy both additive and multiplicative properties of leveled fully homomorphic encryption, security properties, and have the ability to decrypt with the secret key, a BFV ciphertext has three components:
Thus, the BFV encryption scheme for a message π is defined below:
ππ = (Ξ β π + π1 + ππ1 β π’, π2 + ππ2 β π’)
where Ξ is a constant, π1 and π2 are small noise components, ππ1 and ππ2 are two parts of the public key, and π’ is a random value.
For decryption, knowing the secret key π , allows us to add the ciphertext components together in a way that cancels out the public key and leaves the original message with a little noise.
The noise component needs to remain small enough, so that when we divide by the constant Ξ and round to the nearest integer, we obtain the original message π.
Yes. Adding two ciphertexts together increases the noise by a small amount, whereas multiplying two ciphertexts together increases the noise by much more.
If the noise gets too large, the ciphertext will no longer decrypt to the correct message. To ensure this does not happen, if we know the number of additions and multiplications that we wish to perform beforehand, we can choose the encryption parameters in such a way that the noise never gets too large.
Fully homomorphic encryption (FHE) satisfies the additional property that you can perform an unlimited number of additions and multiplications.
The first FHE scheme was invented by Craig Gentry in 2009, when he introduced a procedure known as bootstrapping.
If we can prevent the noise from getting too large, we can perform an unlimited number of computations. The easiest way to remove the noise from a ciphertext before the noise gets too large, is to decrypt it. Getting the exact plaintext result and re-encrypting it will refresh the noise back down to be small.
However, we want to perform all our computations without decrypting it in between.
Luckily researchers have found ways to express decryption circuits fully through additions and multiplications, which is something we can do while staying encrypted! Making sure a decryption circuit is bootstrappable is often the most challenging part of designing a fully homomorphic encryption scheme, but research in the past decade has shown that it is possible.
