Homomorphic encryption, one of many privacy-enhancing technologies (PETs), is a way for a party to perform computations on encrypted data without ever decrypting it.
Homomorphic encryption can be leveraged for a variety of use cases, including:
When I describe these use cases to colleagues , they often ask how homomorphic encryption could possibly be secure if someone can obtain insights from encrypted data. In this blog, we take a closer look at HE use cases and address how to use homomorphic encryption in a privacy-preserving manner.
The key question here is, who is obtaining the insights from the encrypted data?
Alice, the owner of the data, uses her private key to encrypt the data. Bob, the owner of the machine learning (ML) model, has a cloud service where you input your encrypted data and obtain the result of some ML computation. Bob earns money every time someone uses his ML cloud service, so he does not want to share his model with anyone else.
To allow Alice to keep her data encrypted, Bob uses her public evaluation key to run his model homomorphically on her encrypted data. He returns the encrypted result to Alice. Alice can now decrypt the data with her private key, and now Alice obtains new insights on her private data, and Bob can keep his model private. Alice cannot do this without homomorphic encryption because Bob is unwilling to share his ML model with Alice.
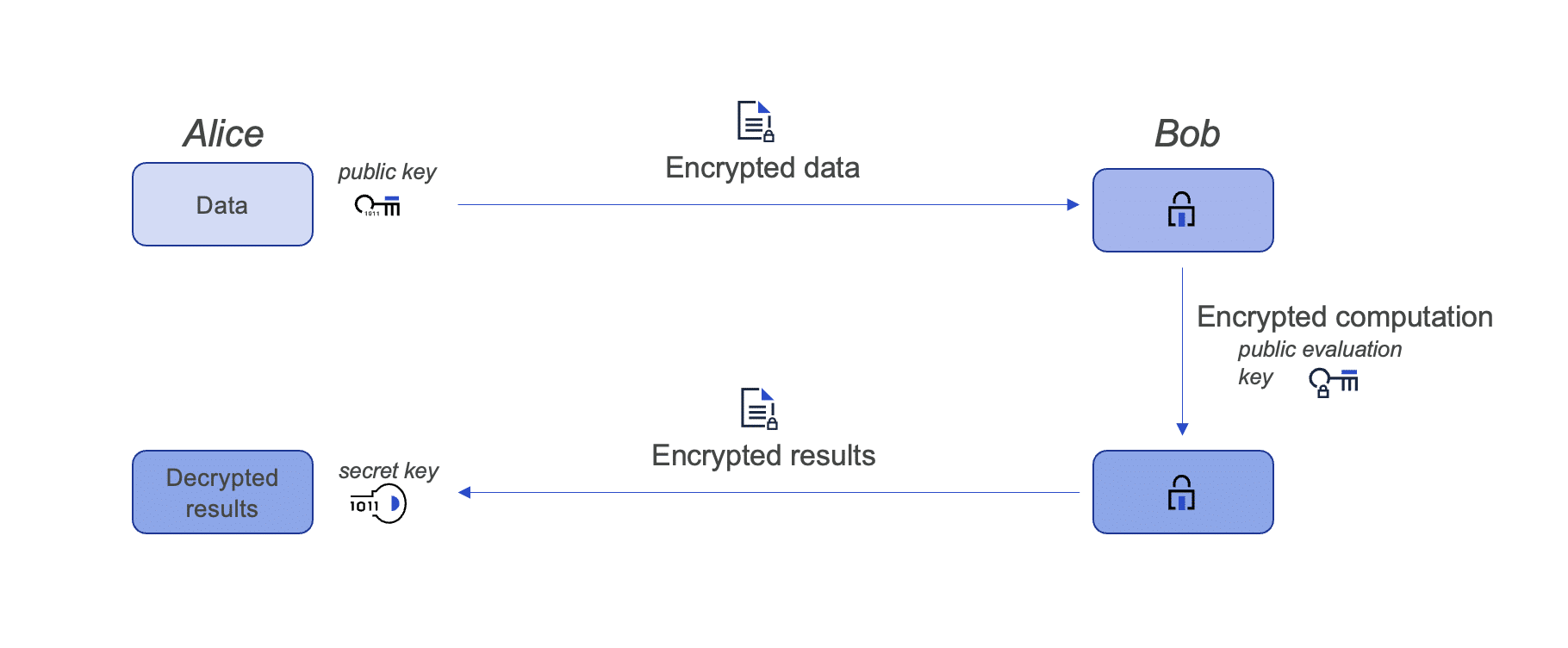
Note that Bob cannot learn anything about the encrypted data or the encrypted computation result. The encrypted data and the encrypted computation both look like gibberish to anyone other than Alice.
If you are interested in a real-world large-scale example of this use case, check out our paper and OpenFHE webinar on large-scale genome-wide association studies.
In this use case, also known as Private Information Retrieval (PIR), Alice is an investor who wants to find the price of a particular stock. Bob maintains a public website which has a list of stocks and their current prices. Alice wants to search the website for her stock price, but she does not want Bob to know which particular stock she is interested in. Downloading the entire database of stocks would allow Alice to maintain privacy but doing this every time a price changes results in very high communication costs.
To allow Alice to keep her query private, Bob assigns a number to every stock in the database. Alice encrypts the stock she wants to query as a vector representing its number. For example, if Alice wants to query the price for stock #3, she encrypts the vector [0, 0, 1, 0, …] with her private key. Using Alice’s public evaluation key, Bob homomorphically multiplies the encrypted vector by his database of stock prices and adds all the values together to obtain the final encrypted stock price which he returns to Alice.
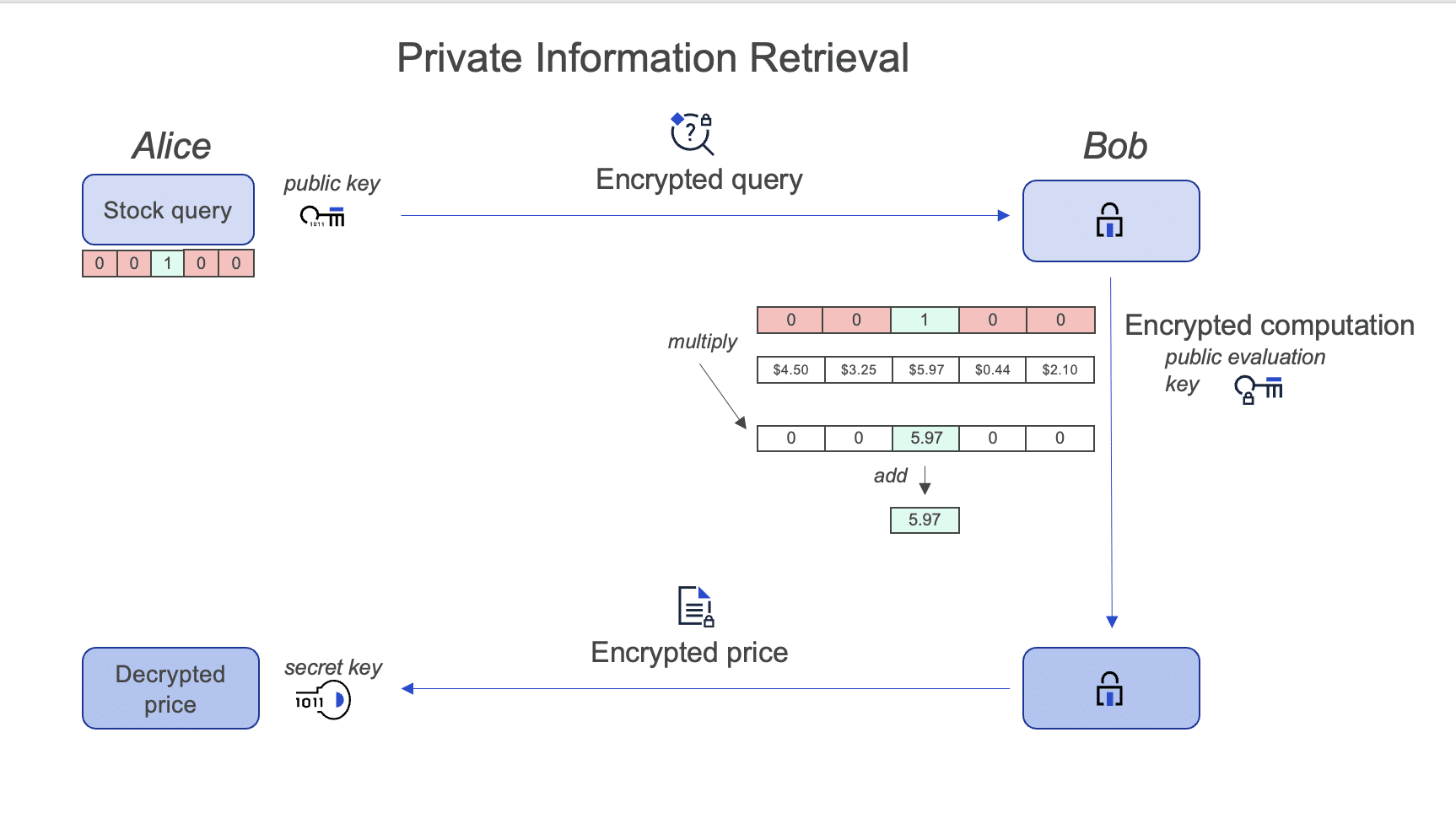
The security of the homomorphic encryption scheme ensures that Bob cannot differentiate between any of the encryptions — whether they are 0, 1, or another value. Homomorphic encryption allows Alice to perform the query privately in a much more efficient manner than downloading the entire database.
If you would like to learn more about PIR, check out Microsoft’s article and SealPIR code. Also note that one can perform more advanced encrypted SQL queries using the query solution in the Duality Platform.
Suppose Alice, Bob, and Charles all own hospitals and each of them have access to their patients’ healthcare data. Each of them has tried using their own hospital’s data to train a machine learning model to predict whether a new patient has a particular disease. However, none of them obtain very accurate results because none of them have enough patient data within a single hospital. They cannot share their data to create a better model because they wish to keep their patients’ data private (and are also required by law to do so).
To train a model on their combined data sets, they combine homomorphic encryption with secret sharing, creating a cryptographic primitive which we call multiparty homomorphic encryption. Alice, Bob, and Charles interactively generate their own secret shares and a joint public key, and none of them ever see the secret key. They each encrypt their data with the joint public key and send it to Daisy. Daisy uses the joint public evaluation key to train a machine learning model on the combined data. She returns the encrypted ML model to Alice, Bob, and Charles, who each compute partial decryptions of the model. They collaborate with the secret sharing protocol to obtain a full decryption of the model without having shared any of their own patients’ data.
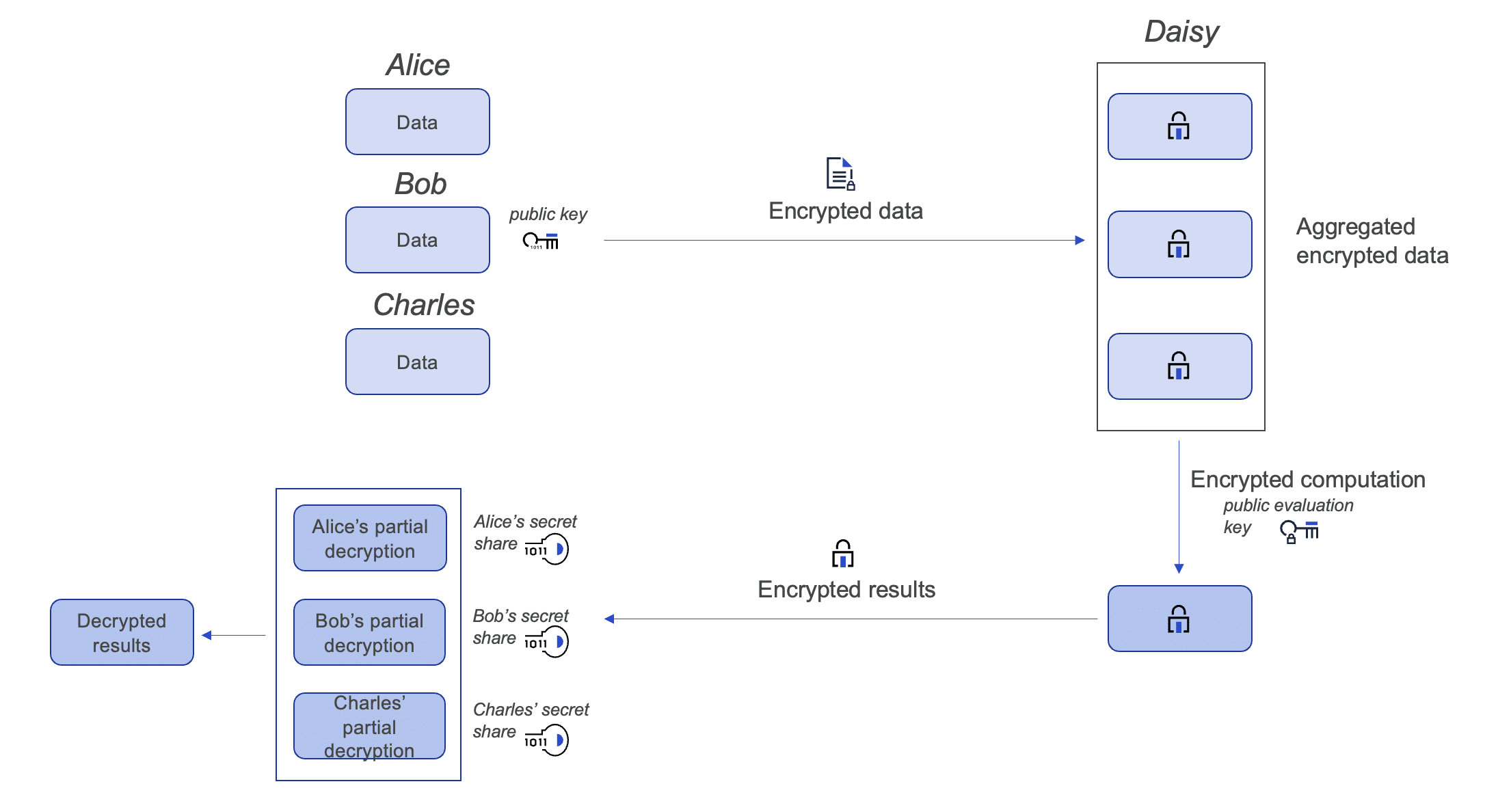
Multiparty homomorphic encryption allows Alice, Bob, and Charles to gain new insights using private data they never see. Note that for this use case, we need to be careful to choose insights that do not leak personally identifiable information (PII) about the data. For example, if the insight returned is the average of all the ages of patients, if Alice and Bob collaborate, they can deduce the average age of all of Charles’ patients. For this use case, combining multiparty homomorphic encryption with differential privacy can further enhance security. To learn more about how to use multiparty homomorphic encryption in C++, check out our OpenFHE webinar.
Want to learn more about how Duality uses homomorphic encryption and other privacy enhancing technologies (PETs) securely for our product use cases? Contact us for a demo of Duality Privacy Preserving Data Collaboration Platform.